几何平均值是啥意思(集中趋势描述)
现如今生活处处有数据,而我们接触到的数据可以分为连续型数据或者离散型数据。
连续型数据的取值范围是一个区间,可以在该区间中连续取值,即连续型数值可以是区间中的任一值,并且一般有度量单位。而离散型数据取值范围是有限个值或者一个数列构成的。
对数据集使用适合的描述指标,能够帮助我们探究庞大、杂乱无序的数据背后隐藏的事实规律。描述数据集的三个维度是指数据的集中趋势描述,数据的离散程度描述和数据的分布形态描述 。
一、集中趋势描述
1.算术平均数 Arithmetic Mean:所有数值的和除以数值的个数。用于描述一组数据在数量上的平均水平。
计算公式:

优缺点:算术平均数是能够充分运用已有信息的代表性数值,每个数值大小的改变都会引起其变化。也因此容易受极值的影响,并且会掩盖数据的差异性。
示例:最近更新了2018年度深圳在岗职工的月平均工资,达到了9309元。这就是一个算术平均值的实际应用。还是要保持进步,争当排头兵而非吊车尾呀。
2.几何平均数 Geometric Mean:对各数值的连乘积开项数次方根。一般用于当总成果为各个阶段(环节)的连乘积时,求各个阶段(环节)的一般成果。
计算公式:

优缺点:几何平均数受极端值的影响比均值小。但仅适用于具有等比或近似等比关系的数据。
示例:连续作业的车间求产品的平均次品率。一个产品的生产由三个环节组成。每个环节都会产生一定的次品。次品率依次为5%、2%、6%,求这个产品的平均次品率。
因为每个环节依次发生,需要完成上一个环节的合格品才能进入下一个环节,所以每个环节的次品率之间是乘积关系。
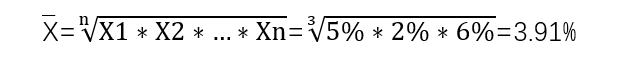
依照上式结果可知,该产品整个生产环节的平均次品率为3.91%。
3.中位数 Median:将数值从小到大依次排列,最中间的数值为中位数。若数值个数为奇数个时,为中间位置的数值;若数值个数为偶数个时,为中间两个数的算术平均数。
优缺点:不受极端值影响,通过损失部分信息,来换取指标的稳定性 。但对极值缺乏敏感性,当样本量小时,中位数不稳定。
示例:毕业生小于获得了两个offer,分别是A、B两个公司。A公司该部门工资情况为甲400元,乙500元,丙600元,丁20000元,B公司该部门工资情况为戊1000元,己1500元,庚2000元,辛8000元。A、B公司平均月薪为5375元、2675元。此时算术平均数受极值影响已失去代表作用,A、B公司月薪中位数550元、1750元能代表更多的数据。
4.众数 Mode:数据中出现次数最多的数值。如果有两个或两个以上的数值出现次数并列最多,那么这些数值都是该数据集的众数。如果所有数值出现的次数相同,这该数据集没有众数。
优缺点:可用于数值型数据,也可用于非数值型数据。数据量越多时越具有代表性,且不受极值影响。
示例:一家销售鞋的商铺,参照以往的消费数据,得出女鞋销售尺码的众数为37码,男鞋销售尺码的众数为42码,那么在商铺备货的时候,女鞋37码和男鞋42码就需要安排更多的备货。
5.截尾均数 Trimmed Mean :将数据进行排序后,按照一定比例去掉两端的数据,只用中部的数据来求均数。若截尾均数与原均数相差不大,说明数据不存在极端值,或者两端极端值的影响正好抵消;若截尾均数与原均数相差较大,则说明数据存在极端值,此时截尾均数可以更好的反应数据的集中趋势。
优缺点:算术平均数较易受到极端值的影响,而截尾均数是其的一种改进,在一定程度上降低极端值给均数带来的影响。
示例:某次艺术比赛10个评委给出评分如下:47、56、74、42、83、75、69、71、76、69。若去掉一个最高分83和一个最低分42,则平均分为:
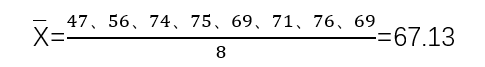
- 伊莱克斯壁挂炉用户售后服务中心实时反馈-今-日-更-新
- 奥莱斯壁挂炉售后号码-全国400服务号码实时反馈-今-日-汇-总
- CMV空调全国各市24小时售后服务点热线号码实时反馈-今-日-汇-总
- 斯諾威热水器客服号码售后号码大全及维修网点查询实时反馈-今-日-更-新
- BORY保险柜售后故障维修客服服务热线是多少实时反馈-今-日-更-新
- 小灵童燃气灶售后维修号码-人工售后号码实时反馈-今-日-更-新
- 鹿峰指纹锁服务热线号码各区24小时维修实时反馈-今-日-汇-总
- 名健壁挂炉全国各市24小时售后服务点热线号码实时反馈全+境+到+达
- 盛凯锅炉全国各市售后服务热线号码实时反馈-今-日-资-讯
- 顾家防盗门全国统一服务号码-全国服务热线实时反馈-今-日-更-新






